Six principes généraux pour déterminer la taille d’échantillon et la puissance statistique

Les évaluations randomisées peuvent fournir des preuves crédibles, transparentes et faciles à expliquer de l'impact d'un programme. Mais pour ce faire, une puissance statistique adéquate et un échantillon suffisamment grand sont essentiels.

La puissance statistique d'une évaluation reflète la probabilité que nous détections tout changement significatif dans un résultat d'intérêt (comme les résultats aux évaluations scolaires ou les comportements de santé) provoqué par un programme réussi. Sans puissance adéquate, une évaluation risque de ne pas nous apprendre grand-chose. Une évaluation randomisée avec une puissance trop faible peut consommer un temps et des ressources monétaires considérables tout en fournissant peu d'informations utiles, ou pire, en ternissant la réputation d'un programme (potentiellement efficace).

Que doivent garder à l'esprit les décideurs politiques et les praticiens pour s'assurer qu'une évaluation a une puissance élevée ? Voici nos six principes généraux pour déterminer la taille d'échantillon et la puissance statistique :

Principe général n°1 : Un échantillon plus grand augmente la puissance statistique de l’évaluation.

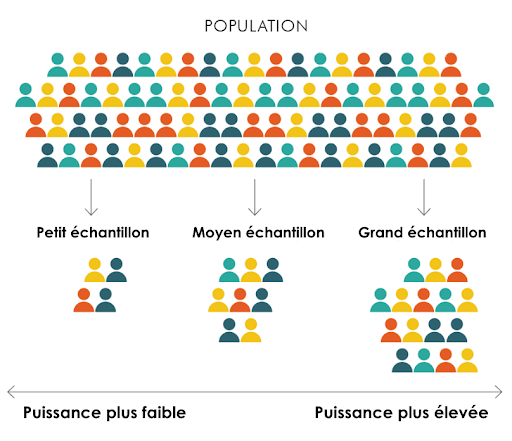
Lors de la conception d'une évaluation, les chercheurs doivent déterminer le nombre de participants de la population générale à inclure dans leur échantillon. Des échantillons plus grands sont plus susceptibles de représenter fidèlement la population d'origine (voir figure ci-dessous) et ont plus de chances de détecter les impacts qui se produiraient dans la population. De plus, des échantillons plus grands augmentent la précision des estimations d'impact et la puissance statistique de l'évaluation. 

Principe général n°2 : Si l’effet d’un programme est faible, l'évaluation nécessite un échantillon plus grand pour atteindre un niveau de puissance donné.

La taille de l'effet d'une intervention correspond à l'ampleur de son impact sur un résultat d'intérêt. Par exemple, l'effet d'un programme de tutorat sur les élèves pourrait être une augmentation de 3 % des résultats aux évaluations de mathématiques. Si un programme a des effets importants, ceux-ci peuvent être détectés avec précision avec des échantillons plus petits, tandis que des effets plus petits nécessitent des échantillons plus grands. Un échantillon plus grand réduit l'incertitude dans nos résultats, ce qui nous donne plus de confiance que les effets détectés (même s'ils sont petits) peuvent être attribués au programme lui-même et non au hasard.

Principe général n°3 : Une évaluation d'un programme avec une faible participation nécessite un échantillon plus grand.

Les évaluations randomisées sont conçues pour détecter l'effet moyen d'un programme sur l'ensemble du groupe de traitement. Cependant, imaginez que seulement la moitié des personnes du groupe de traitement participent réellement au programme. Ce faible taux de participation diminue l'ampleur de l'effet moyen du programme. Puisqu'un échantillon plus grand est nécessaire pour détecter un effet plus petit (voir principe général n°2), il est important de planifier à l'avance si une faible participation est anticipée et de mener l'évaluation avec un échantillon plus large.

Principe général n°4 : Si l’indicateur de résultat prend des valeurs très dispersées dans la population, l'évaluation nécessite un échantillon plus grand.

Dans la population, il peut y avoir une variance élevée ou faible dans les mesures d’indicateurs clés pour le programme en question. Par exemple, considérons un programme conçu pour réduire l'obésité, mesurée par l'Indice de Masse Corporelle (IMC), chez les participants. Si la population a des IMC à peu près similaires, en moyenne au début du programme, il est plus facile d'identifier l'impact causal du programme parmi les participants du groupe de traitement. Vous pouvez être assez confiant qu'en l'absence du programme, la plupart des membres du groupe de traitement auraient connu des changements similaires d'IMC au fil du temps.

Cependant, si les participants présentent une grande variation d'IMC au début du programme, il devient plus difficile d'isoler les effets du programme. L'IMC moyen du groupe aurait pu changer en raison d'une variation naturelle au sein de l'échantillon, plutôt qu'en raison du programme lui-même. En particulier lors de l'évaluation d'une population à forte variance, sélectionner un échantillon plus grand augmente la probabilité que vous puissiez distinguer l'impact du programme de l’effet de la variation aléatoire dans ces mesures de résultats.

Principe général n°5 : Pour une taille d’échantillon donnée, la puissance est optimale lorsque l’échantillon est équitablement réparti entre le groupe traitement et le groupe contrôle.

Pour atteindre une puissance optimale pour une taille d’échantillon donnée, l'échantillon doit être divisé de manière équitable entre le groupe de traitement et le groupe de contrôle. Si vous ajoutez des participants à l'étude, la puissance augmentera que vous les ajoutiez au groupe de traitement ou au groupe de contrôle, car la taille de l'échantillon total augmente. Cependant, la manière la plus efficace d'augmenter la puissance en augmentant la taille de l'échantillon est d'ajouter des participants pour atteindre ou maintenir un équilibre entre les groupes de traitement et de contrôle.

Principe général n°6 : Pour une taille d'échantillon donnée, randomiser au niveau des grappes d’observations plutôt qu'au niveau individuel réduit la puissance de l'évaluation. Plus les résultats d’intérêt des individus au sein des grappes sont similaires, plus l'échantillon doit être grand.

Lors de la conception d'une évaluation, l'équipe de recherche doit choisir l'unité de randomisation. L'unité de randomisation peut être un participant individuel ou une “grappe” (un “cluster”). Les grappes représentent des ensembles d'individus (tels que les ménages, les quartiers ou les villes) qui sont traités comme des unités distinctes, et chaque grappe est assignée de manière aléatoire au groupe de traitement ou de contrôle.

Pour une taille d'échantillon donnée, la randomisation de grappes plutôt que d'individus diminue la puissance de l'étude. En général, le nombre de grappes est un facteur plus important pour la puissance que le nombre d’individus par grappe. Par conséquent, si vous souhaitez augmenter la taille de votre échantillon, et que les individus au sein d'une grappe sont similaires les uns aux autres sur le résultat d'intérêt, la façon la plus efficace d'augmenter la puissance de l'évaluation est d'augmenter le nombre de grappes plutôt que d'augmenter le nombre de participants par grappe. Par exemple, dans l'exemple du programme contre l'obésité du principe général n°4, ajouter plus de ménages serait une façon plus efficace d'augmenter la puissance que d'augmenter le nombre d'individus par ménage, en supposant que les individus au sein des ménages ont des mesures d'IMC similaires.

Vous avez encore des questions ? Lisez notre courte publication, qui détaille la façon de suivre ces principes généraux pour vous assurer que votre évaluation a une puissance adéquate.