
Six rules of thumb for understanding statistical power
Randomized evaluations can provide credible, transparent, and easy-to-explain evidence of a program’s impact. But in order to do so, adequate statistical power and a sufficiently large sample are essential.
The statistical power of an evaluation reflects how likely we are to detect any meaningful changes in an outcome of interest (like test scores or health behaviors) brought about by a successful program. Without adequate power, an evaluation may not teach us much. An underpowered randomized evaluation may consume substantial time and monetary resources while providing little useful information, or worse, tarnishing the reputation of a (potentially effective) program.
What should policymakers and practitioners keep in mind to ensure that an evaluation is high powered? Read our six rules of thumb for determining sample size and statistical power:
Rule of thumb #1: A larger sample increases the statistical power of the evaluation.
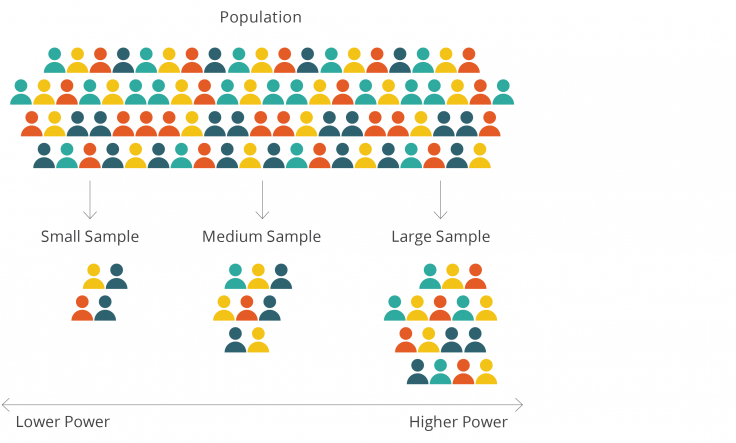
When designing an evaluation, researchers must determine the number of participants from the larger population to include in their sample. Larger samples are more likely to be representative of the original population (see figure below) and are more likely to capture impacts that would occur in the population. Additionally, larger samples increase the precision of impact estimates and the statistical power of the evaluation.
Rule of thumb #2: If the effect size of a program is likely to be small, the evaluation needs a larger sample to achieve a given level of power.
The effect size of an intervention is the magnitude of the impact of the intervention on a particular outcome of interest. For example, the effect of a tutoring program on students might be a three percent increase in math test scores. If a program has large effects, these can be precisely detected with smaller samples, while smaller effects require larger sample sizes. A larger sample reduces uncertainty in our findings, which gives us more confidence that the detected effects (even if they’re small) can be attributed to the program itself and not random chance.
Rule of thumb #3: An evaluation of a program with a low participation rate needs a larger sample.
Randomized evaluations are designed to detect the average effect of a program over the entire treatment group. However, imagine that only half the people in the treatment group actually participate in the program. This low participation rate decreases the magnitude of the average effect of the program. Since a larger sample is required to detect a smaller effect (see rule of thumb #2), it is important to plan ahead if low take-up is anticipated and run the evaluation with a larger sample.
Rule of thumb #4: If the underlying population has high variation in outcomes, the evaluation needs a larger sample.
In a given evaluation sample, there may be high or low variation in characteristics that are relevant to the program in question. For example, consider a program designed to reduce obesity, as measured by Body Mass Index (BMI), among participants. If the population has roughly similar BMIs, on average at program start, it is easier to identify the causal impact of the program among treatment group participants. You can be fairly confident that absent the program, most members of the treatment group would have seen similar changes in BMI over time.
However, if participants have wide variation in BMIs at program start, it becomes harder to isolate the program’s effects. The group’s average BMI might have changed due to naturally occurring variation within the sample, rather than as a result of the program itself. Especially when running an evaluation of a population with high variance, selecting a larger sample increases the likelihood that you will be able to distinguish the impact of the program from the impact of naturally occurring variation in key outcome measures.
Rule of thumb #5: For a given sample size, power is maximized when the sample is equally split between the treatment and control group.
To achieve maximum power, the sample should be evenly divided between treatment and control groups. If you add participants to the study, power will increase regardless of whether you add them to the treatment or control group because the overall sample size is increasing. However, the most efficient way to increase power when expanding the sample size is to add participants to achieve or maintain balance between the treatment and control groups.
Rule of thumb #6: For a given sample size, randomizing at the cluster level as opposed to the individual level reduces the power of the evaluation. The more similar the outcomes of individuals within clusters are, the larger the sample needs to be.
When designing an evaluation, the research team must choose the unit of randomization. The unit of randomization can be an individual participant or a “cluster.” Clusters represent groups of individuals (such as households, neighborhoods, or cities) that are treated as distinct units, and each cluster is randomly assigned to the treatment or control group.
For a given sample size, randomizing clusters as opposed to individuals decreases the power of the study. Usually, the number of clusters is a bigger determinant of power than the number of people per cluster. Therefore, if you are looking to increase your sample size, and individuals within a cluster are similar to each other on the outcome of interest, the most efficient way to increase the power of the evaluation is to increase the number of clusters rather than increasing the number of people per cluster. For instance, in the obesity program example from rule of thumb #4, adding more households would be a more efficient way to increase power than increasing the number of individuals per household, assuming individuals within households have similar BMI measures.
Still have questions? Read our short publication, which goes into further detail on how to follow these rules of thumb to ensure that your evaluation has adequate power.

